Bangun Datar
Berdasarkan yang disebutkan oleh wikipedia, bangun datar merupakan sebutan untuk berbagai bangun dua dimensi.
Bangun datar diantaranya seperti: lingkaran, belah ketupat, layang-layang, trapesium, jajar genjang, segitiga, persegi panjang serta persegi.
Pada tiap-tiap bangun tersebut memiliki rumus untuk menghitung luas sekaligus keliling yang berbeda satu bangun dengan bangun yang lain.
Selengkapnya mengenai bidang datar, simak baik-baik ulasan di bawah ini.
Bangun Datar
Melengkapi uraian di atas, bangun datar merupakan suatu bagian dari bidang datar yang dibatasi oleh garis-garis lurus atau lengkung.
Definisnya sendiri secara rinci ialah: suatu bangun yang memiliki bidang rata serta mempunyai dua dimensi yakni panjang dan lebar namun tidak mempunyai tinggi dan tebal.
Rumus Bangun Datar
Berikut ini akan kami berikan macam atau jenis dari bangun datar beserta sifatnya. Perhatikan ulasan di bawah ini.
1. Persegi
Pengertian Persegi
Persegi merupakan suatu bangun datar 2 dimensi yang terbentuk oleh 4 buah rusuk dengan memiliki ukuran sama panjang serta memiliki 4 buah sudut siku – siku.
Persegi juga bisa kita sebut sebagai bangun datar yang mempunyai sisi sisi sama panjang serta sudut sudut sama besar.
Sifat Persegi
Seluruh sisi-sisinya memiliki ukuran panjang yang sama serta seuruh sisinya berhadapan sejajar.
Masing-masing sudut yang dimilikinya adalah sudut siku-siku.
Memiliki dua diagonal dengan ukuran panjang yang sama sama serta berpotongan di tengah-tengah dan membentuk sudut siku-siku.
Pada masing-masing sudutnya di bagi dua sama besarnya oleh diagonalnya.
Memiliki empat buah sumbu simetri.
Rumus yang ada pada Persegi
Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun persegi, antara lain:
Rumus luas persegi, yaitu:
L = S x S
Rumus keliling persegi, yaitu:
K = S + S + S + S
ataupun K = 4 x S
Keterangan:
L: Luas
K: Keliling
S: Sisi
Contoh Soal:
Perhatikanlah gambar di bawah ini:
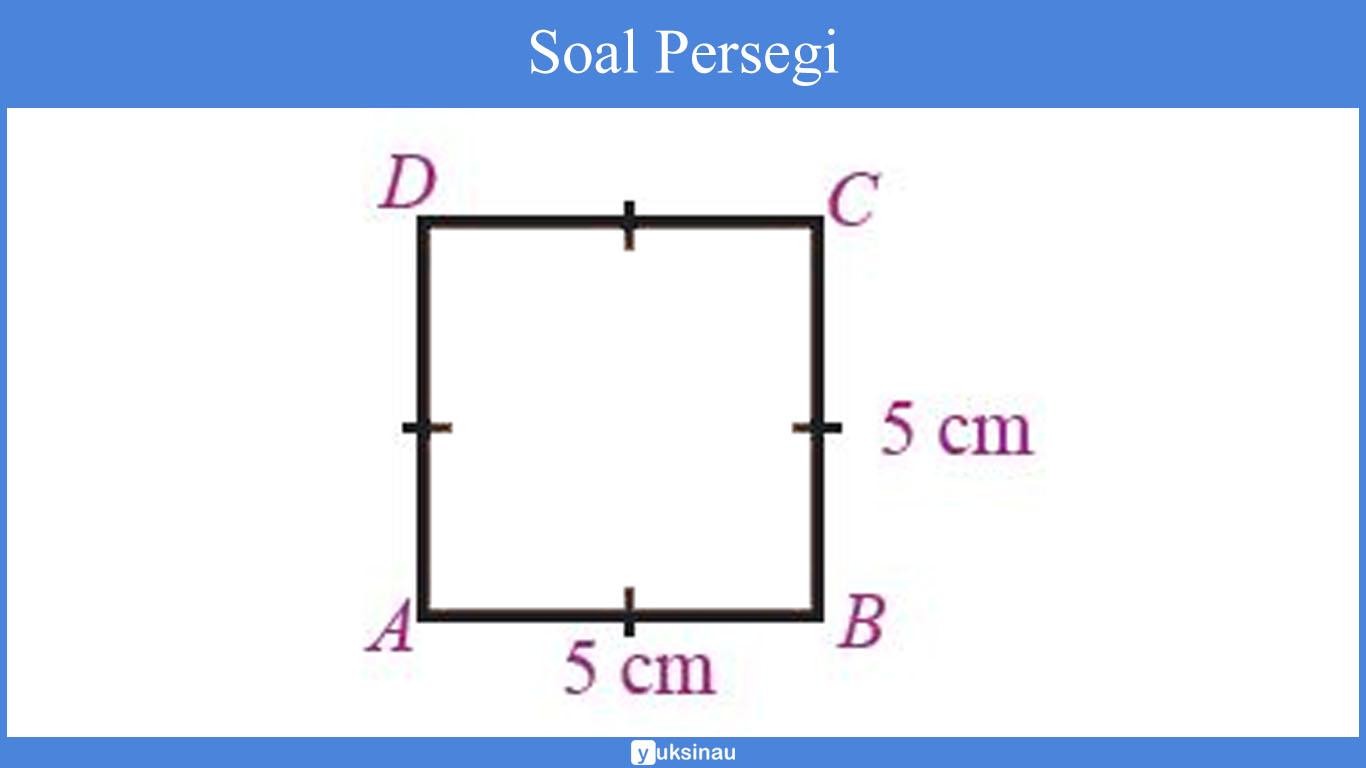
tentukan:
a. Tentukan luas perseginya:
b. Tentukan keliling perseginya:
Jawab:
a. Rumus Luas persegi ABCD yakni: s x s, sehingga
= 5 cm x 5 cm
= 25 cm2.
Jadi, luas persegi ABCD yaitu: 25 cm2.
b. Rumus Keliling persegi ABCD ialah: 4 x s, sehingga
= 4 x 5 cm
= 20 cm.
Jadi, jumlah keliling persegi ABCD tersebut yaitu 20 cm.
2. Persegi Panjang
Pengertian Persegi Panjang
Persegi panjang meurpakan suatu bangun datar 2 dimensi yang terbentuk oleh 2 buah pasang rusuk yang panjang serta sejajar dan memiliki 4 buah sudut siku – siku.
Sifat Bangun Datar Persegi Panjang
Masing-masing sisi-sisi yang berhadapan memiliki ukuran sama panjang dan juga sejajar.
Seluruh sudutnya merupakan sudut siku-siku.
Mempunyai dua buah diagonal yang sama panjang serta saling berpotongan di titik pusat bangun persegi panjang.
Titik tersebut adalah membagi dua bagian diagonal dengan ukuran sama panjang.
Mempunyai dua buah sumbu simetri yakni sumbu vertikal dan juga sumbu horizontal.
Rumus yang ada pada Bangun Datar
Persegi Panjang
Rumus luas persegi panjang, yaitu:
L = p x l
Rumus keliling persegi panjang, yaitu:
K = 2 x (p + l)
Keterangan:
L: Luas
K: Keliling
p: panjang
l: lebar
Contoh Soal
Suatu bangun persegi panjang, mempunyai p = 10 cm dan l = 5 cm,
terdiri atas EFGH:
Pertanyaan:
a. Hitunglah luas persegi panjang EFGH:
b. Hitunglah keliling persegi panjang EFGH!:
Jawab:
a. Rumus luas persegi panjang EFGH adalah L= p x l,
sehingga
L = 10 cm x 5 cm
L = 50 cm2.
Jadi, luas persegi panjang EFGH yaitu 50 cm2.
b. Rumus Keliling sama persegi panjang EFGH adalah: 2 x (p + l),
sehingga
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm
Jadi, keliling persegi panjang EFGH yaitu 50 cm.
3. Segitiga
Pengertian Bangun Datar Segitiga
Segitiga merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 3 buah sisi yang berwujud garis lurus serta 3 buah sudut.
Sehingga bangun datar yang terbentuk dari tiga atau lebih garis lurus disebut sebagai segitiga.
Segitiga juga menjadi bangun datar yang penting dalam sebuah desain rumah, bagi kamu yang ingin melihat referensi rumah indah impian maka bisa kunjungi ruangarsitek.id
Sifat Bangun Datar Segitiga
Pada bangunan segitiga, ketiga sudutnya memiliki besaran 180º. (jika dijumlahkan hasilnya 180)
Sifat Segitiga mempunyai 3 sisi serta 3 titik sudut.
Rumus yang ada pada Bangun Datar Segitiga
Rumus luas segitiga
yaitu:
Luas = ½ x a x t
Rumus keliling segitiga yaitu:
Keliling = s + s + s
atau K = a + b + c
Contoh Soal
Suatu bangun segitiga memiliki sebuah ukuran seperti yang tertera di gambar di bawah ini:
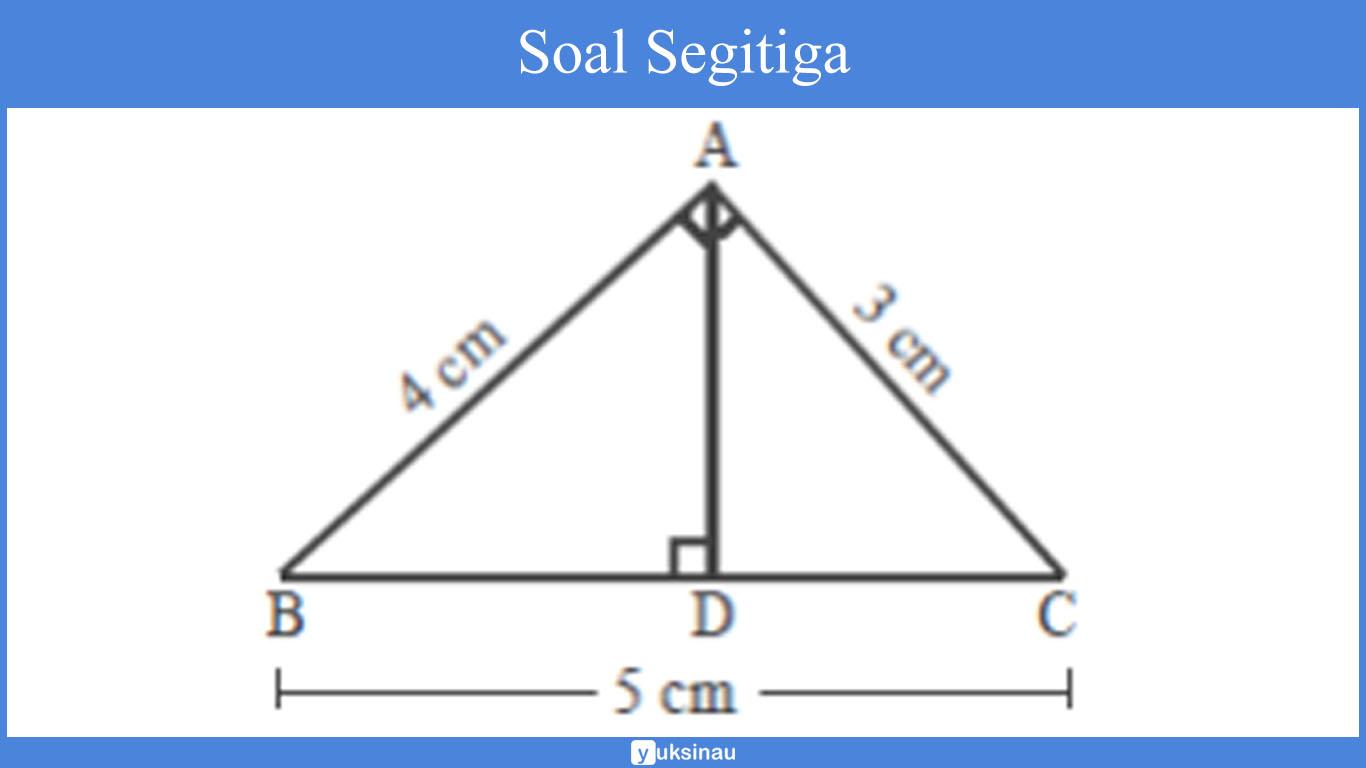
a. Hitunglah luas segitiga :
b. Hitunglah keliling segitiga :
Jawab:
a. Luas segitiga Rumusnya yaitu ½ x a x t, sehingga
= ½ x 3 cm x 4 cm
= ½ x 12 cm2.
= 6 cm2
Jadi, hasil perhitungan dari luas segitiga adalah 6 cm2.
b. Keliling segitiga nya adalah = s + s + s, sehingga
= AC+AB+BC
= 3cm+4cm+5cm
= 12 cm.
Jadi, keliling segitiga adalah 12 cm.
4. Jajar genjang
Pengertian Bangun Datar Jajar genjang
Pengertian dari jajar genjang sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk atas 2 buah pasang rusuk yang di mana pada masing – masing nya memiliki ukuran sama panjang serta sejajar dengan pasangan nya.
Kemudian jajar genjang memiliki 2 buah pasang sudut siku – siku yang di mana pada masing – masing sudutnya sama besar dengan sudut di depan nya.
Sifat Bangun Datar Jajar genjang
Sifat pada Jajar Genjang tidak memiliki simetri lipat.
Jajar Genjang memiliki simetri putar tingkat dua.
Sudut Jajar Genjang yang berhadapan memiliki ukuran yang sama besar.
Jajar Genjang memiliki 4 sisi serta 4 sisi sudut.
Diagonal yang dimilikinya memiliki panjang yang tidak sama.
Jajar Genjang memiliki 2 Pasang Sisi yang sejajar serta sama panjang.
Jajar Genjang memiliki 2 buah sudut tumpul dan 2 buah sudut lancip.
Rumus yang ada pada Bangun Datar Jajar genjang
Contoh Soal
| Nama | Rumus |
| Keliling (Kll) | Kll = 2 × (a + b) |
| Luas (L) | L = a × t |
| Sisi Alas (a) | a = (Kll ÷ 2) – b |
| Sisi Sisi Miring (b) | a = (Kll ÷ 2) – a |
| t diketahui L | t = L ÷ a |
| a diketahui L | a = L ÷ t |
Perhatikanlah gambar jajaran genjang ABCD di bawah ini!
Panjang BC = DA = 8 cm.
Pertanyaan:
a. Hitunglah luas jajaran genjang ABCD, merupakan:
b. Hitunglah keliling jajaran genjang ABCD, merupakan:
Jawab:
a. Luas jajaran genjang ABCD adalah = a x t, sehingga
= 8 cm x 7 cm
= 56 cm2
Jadi, luas jajaran genjang ABCD yaitu 56 cm2.
b. Keliling jajaran genjang ABCD adalah s + s + s + s, maka:
K = AB + BC + CD + DA, yakni :
K = 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm.
Jadi, keliling jajaran genjang ABCD adalah 32 cm.
5. Trapesium
Pengertian Bangun Datar Trapesium
Pengertian dari trapesium sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk dari 4 buah rusuk yang 2 buah di antaranya merupakan saling sejajar namun panjang nya tidak sama.
Tetapi terdapat juga trapesium yang rusuk ketiganya merupakan tegak lurus pada rusuk – rusuk sejajar nya yang biasa dikenal dengan sebutan trapesium siku – siku.
Sifat Bangun Datar Trapesium
Trapesium adalah bangun datar dengan 4 sisi (quadrilateral).
Memiliki 2 sisi sejajar yang tidak sama panjang.
Memiliki 4 buah titik sudut.
Minimal pada bagun datar trapesium memiliki 1 titik sudut tumpul
Trapesium memiliki 1 simetri putar.
Rumus yang ada pada Bangun Datar Trapesium
Contoh soal:
| Nama | Rumus |
| Luas (L) |  |
| Keliling (Kll) | Kll = AB + BC + CD + DA |
| Tinggi (t) |  |
| Sisi a (CD) |  atau CD = Kll – AB – BC – AD |
| Sisi b (AB) |  atau AB = Kll – CD – BC – AD |
| Sisi AD | AD = Kll – CD – BC – AB |
| Sisi BC | BC = Kll – CD – AD – AB |
Perhatikanlah bangun datar trapesium EFGH di bawah ini!
Panjang EH = FG ialah 8 cm.
Pertanyaan:
a. Tentukanlah luas trapesium EFGH:
b. Tentukanlah keliling trapesium EFGH:
Jawab:
a. Luas trapesium EFGH adalah: ½ x (a + b) x t maka,
= ½ x (16cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11cm x 7 cm
= 77 cm2
Jadi, luas trapesium EFGH di atas adalah 77 cm2.
b. Keliling trapesium EFGH memiliki rumus yaknni: s + s + s + s, maka:
K = EF + FG + GH + HE
K = 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.
Jadi, luas keliling trapesium EFGH di atas adalah 38 cm.
6. Layang – layang
Pengertian dari layang – layang sendiri merupakan suatu bangun datar 2 dimensi yang di bentuk oleh 2 buah segitiga sama kaki serta berbentuk segiempat di mana memiliki alas yang berhimpitan dan berbentuk menjadi suatu layang – layang.
Memiliki 2 pasangan sisi yang membentuk sudut yang berbeda.
Pasangan 1 merupakan sisi a dan b, membentuk sudut ∠ABC.
Pasangan 2 merupakan sisi c dan d, membentuk sudut ∠ADC.
Memiliki sepasang sudut yang saling berhadapan dengan besar ukuran yang sama.
Sudut ∠BAD serta ∠BCD saling berhadapan dan memiliki besar yang sama.
Memiliki 2 diagonal dengan panjang yang berbeda.
Diagonal layang-layang saling tegak lurus (90º).
Diagonal terpanjang adalah sumbu simetri layang-layang.
Layang-layang hanya mempunyai 1 sumbu simetri.
Rumus yang ada pada Bangun Datar Layang – layang
Contoh Soal
Perhatikan layang layang ABCD di bawah ini!
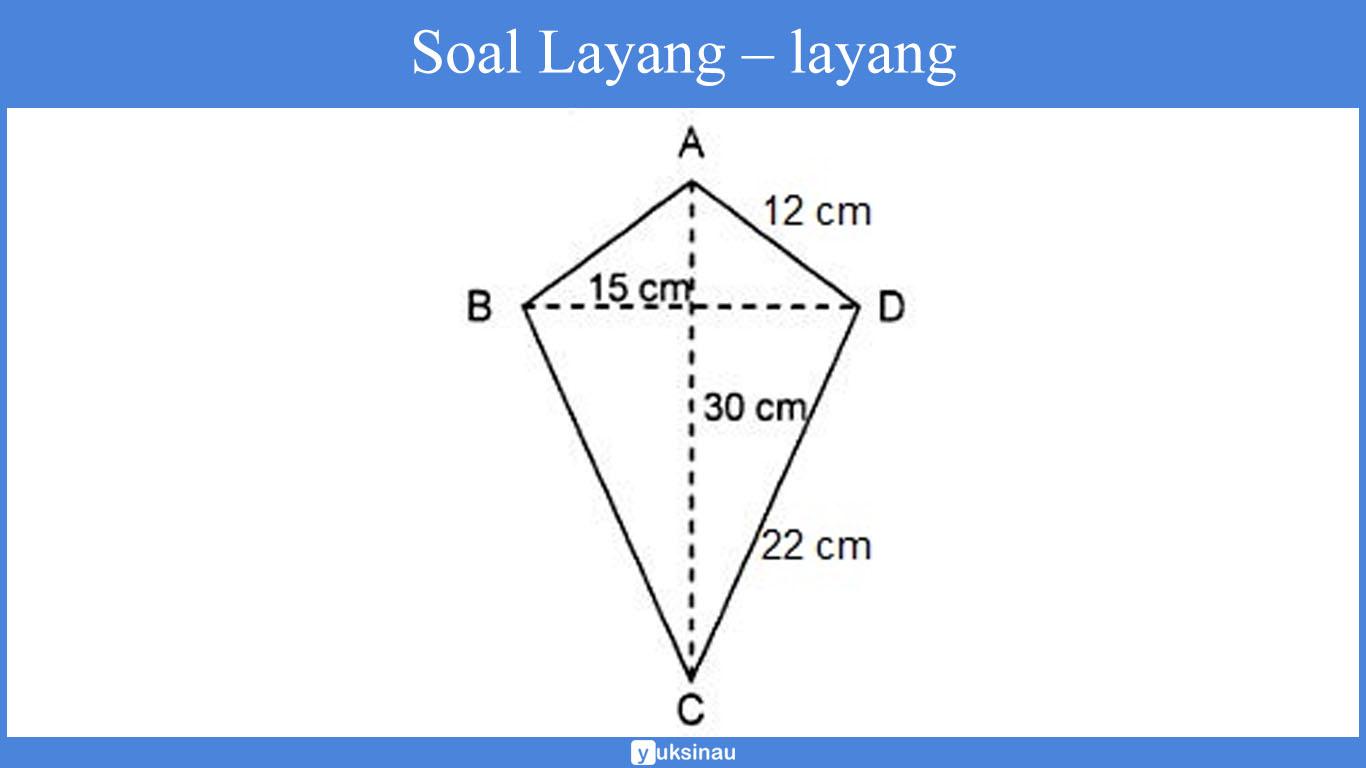Diketahui;
| Nama | Rumus |
| Luas (L) | L = ½ × d1 × d2 |
| Keliling (Kll) | Kll = a + b + c + d |
| Kll = 2 × (a + c) | |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
| a atau b | a = (½ × Kll) – c |
| c atau d | c = (½ × Kll) – a |
Panjang BC = panjang CD
Panjang AB = panjang AD
Pertanyaan:
a. Hitunglah luas layang layang ABCD!
b. Hitunglah keliling layang layang ABCD!
Jawab:
a. Luas layang-layang ABCD adalah = ½ x d1 x d2, sehingga
= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2
Jadi, luas layang layang ABCD tersebut yaitu 225 cm2.
b. Keliling dari layang-layang ABCD adalah: 2 x (x + y), sehingga
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm
Jadi, keliling layang layang ABCD yaitu 68 cm.
7. Belah Ketupat
Belah Ketupat merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 4 buah sisi dengan ukuran sama panjang serta memiliki 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan memiliki besar sama.
Dalam bahasa inggris, belah ketupat disebut sebagai rhombus.
Sifat Bangun Datar Belah Ketupat
Keempat sisinya sama panjang.
Memiliki 2 diagonal yang saling tegak lurus.
Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°).
Sudut yang saling berhadapan memiliki besar yang sama.
Pada belah ketupat sudut yang berhadapan memiliki besar yang sama. Ilustrasi di atas menunjukkan besar sudut ∠ABC = ∠ADC dan ∠BAD = ∠BCD.
Besar pada keempat titik sudutnya 360º.
Memiliki 2 sumbu simetri yang di mana adalah diagonalnya.
Belah Ketupat memiliki Simetri Putar tingkat 2.
Memiliki 4 buah sisi dan 4 buah titik sudut.
Keempat sisi belah ketupat mempunyai panjang yang sama.
Rumus yang ada pada Bangun Datar Belah Ketupat
Contoh Soal:
| Nama | Rumus |
| Keliling (Kll) | Kll = s + s + s + s |
| Kll = s × 4 | |
| Luas (L) | L = ½ × d1 × d2 |
| Sisi (s) | s = Kll ÷ 4 |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
Perhatikan belah ketupat di bawah ini!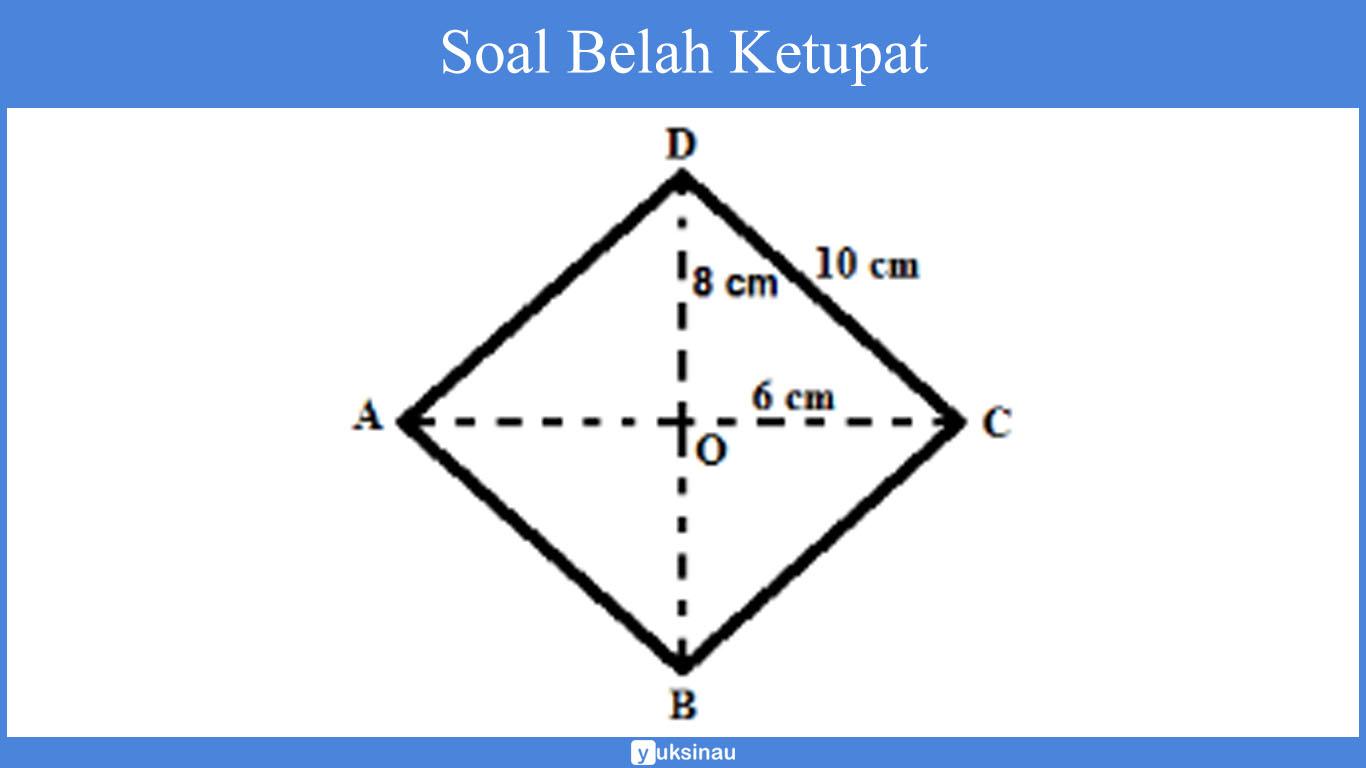
Panjang AC adalah 12 cm
Panjang BD adalah 16 cm
Pertanyaannya yaitu:
a. Tentukanlah luas belah ketupat ABCD!
b. Tentukan simak keliling belah ketupat ABCD!
Jawab:
a. Luas belah ketupat ABCD adalah = ½ x d1 x d2, sehingga
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2
Jadi, luas belah ketupat ABCD yaitu 96 cm2.
b. Keliling belah ketupat ABCD adalah: s + s + s + s,
sehingga
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm
Jadi, keliling belah ketupat ABCD yaitu 40 cm.
8.
sumber : https://www.yuksinau.id/bangun-datar/
SOAL LATIHAN - Suatu persegi panjang memiliki panjang 28 cm dan lebar 9 cm, maka luasnya adalah .... cm²
- Luas suatu persegi panjang adalah 128 cm² . Jika panjangnya 16 cm, maka lebarnya adalah .... cm
- Selembar kain dengan ukuran panjang 150 cm dan lebarnya 75 cm. Keliling kain tersebut adalah .... cm.
- Keliling persegi panjang 88 cm. Jika panjangnya 26 cm, maka lebarnya adalah .... cm
- Teras rumah Pak Rudi luasnya 18 m² akan dipasang ubin berukuran 25 cm x 20 cm. Banyaknya ubin yang dibutuhkan adalah .... ubin
- Kebun kakek berbentuk persegi panjang berukuran panjang 75 meter dan lebar 45 meter. Di sekeliling kebun akan dipasang pagar dengan biaya Rp 115.000,00 per meter. Biaya yang diperlukan untuk pemasangan pagar tersebut adalah ....
- Sebuah kolam renang berbentuk persegi panjang memiliki panjang 40 meter dan lebar 20 meter. Kolam renang tersebut dikelilingi jalan setapak selebar 1 meter. Luas jalan setapak itu adalah .... m²
- Keliling sebuah kebun 160 m. Jika panjang kebun 50 m, maka lebar kebun tersebut adalah ....
- Pekarangan belakang rumah paman berbentuk persegi panjang berukuran panjang 68 meter dan lebar 45 meter akan dibuatkan pagar dari bambu. Tiap meter membutuhkan 3 bambu. Banyaknya bambu yang dibutuhkan untuk membuat pagar pekarangan adalah ....
- Sebuah halaman berbentuk persegi panjang, kelilingnya 210 m dan lebarnya 35 m. Luas halaman tersebut adalah .... m²
- Keliling suatu persegi panjang adalah 80 cm dan lebarnya 12 cm kurang dari panjangnya. Maka panjang dan lebar persegi panjang tersebut adalah ....
- Ayah membuat papan tulis berukuran 200 cm x 150 cm. Papan tulis tersebut membutuhkan 2 kaleng cat berukuran kecil untuk tiap m². Cat yang dibutuhkan ayah untuk mengecat papan tulis tersebut adalah .... kaleng.
Komentar
Posting Komentar